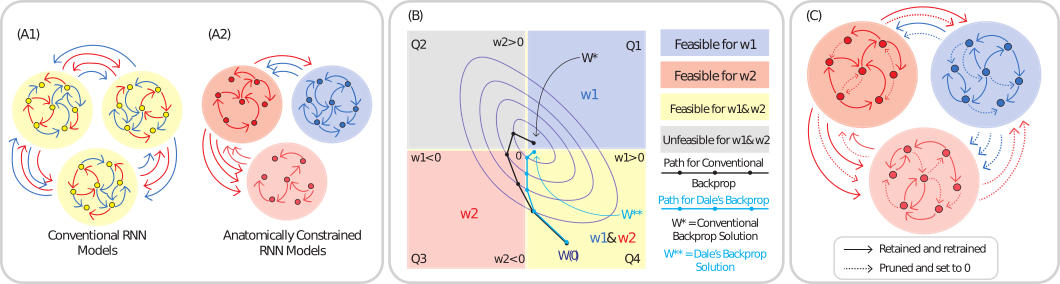
Schematic for constructing biologically constrained RNNs

Schematic for constructing biologically constrained RNNs. (A) Illustration of conventional vs. biologically constrained RNN models (A1 vs. A2). Conventional RNNs consist of general purpose neurons that project a mix of excitatory and inhibitory signals, with no specific connectivity structure within or across populations. Biologically constrained RNNs restrict populations of neurons to be either strictly excitatory (red) or inhibitory (blue), with anatomically-informed connectivity motifs both within and across populations. (B) Optimization in parameter space when training with conventional backpropagation (black) vs. Dale's backprop (blue). Purple contours represent level sets for the positions the algorithms take in parameter space at different time steps. (C) Enforcing anatomically-consistent connectivity motifs. Dashed lines represent connections that are set to 0 during the pruning process. Solid lines represent connections that are retained post-pruning.

Abstract

Recurrent neural networks (RNNs) have emerged as a prominent tool for modelling cortical function, and yet their conventional architecture is lacking in physiological and anatomical fidelity. In particular, these models often fail to incorporate two crucial biological constraints: i) Dale's law, i.e., sign constraints that preserve the ``type'' of projections from individual neurons, and ii) Structured connectivity motifs, i.e., highly sparse yet defined connections amongst various neuronal populations. Both constraints are known to impair learning performance in artificial neural networks, especially when trained to perform complicated tasks; but as modern experimental methodologies allow us to record from diverse neuronal populations spanning multiple brain regions, using RNN models to study neuronal interactions without incorporating these fundamental biological properties raises questions regarding the validity of the insights gleaned from them. To address these concerns, our work develops methods that let us train RNNs which respect Dale's law whilst simultaneously maintaining a specific sparse connectivity pattern across the entire network. We provide mathematical grounding and guarantees for our approaches incorporating both types of constraints, and show empirically that our models match the performance of RNNs trained without any constraints. Finally, we demonstrate the utility of our methods on 2-photon calcium imaging data by studying multi-regional interactions underlying visual behaviour in mice, whilst enforcing data-driven, cell-type specific connectivity constraints between various neuronal populations spread across multiple cortical layers and brain areas. In doing so, we find that the results of our model corroborate experimental findings in agreement with the theory of predictive coding, thus validating the applicability of our methods.

Instructions

The following folders can be used to replicate results corresponding to the following figures from the paper Constructing Biologically Constrained RNNs via Dale’s Backpropagation and Topologically-Informed Pruning.